高中如何学好数学?各题型详细方法总结+100个核心考点全汇总!

3.直译法
顾名思义,就是直接翻译题目中的条件。将题目中的文字用数学方程表达出来即可。
4.相关点法
假如题目中已知动点P的轨迹,另外一个动点M的坐标与P有关系,可根据此关系,用M的坐标表示P的坐标,再带入P的满足的轨迹方程,化简即可得到M的轨迹方程。

5.参数法
当动点坐标x、y之间的直接关系难以找到时,可以先找到x、y与另一参数t的关系,得再消去参变数t,得到轨迹方程。

6.交轨法
若题目中给出了两个曲线,求曲线交点的轨迹方程时,应将两动曲线方程中的参数消去,得到不含参数的方程,即为两动曲线交点的轨迹方程。

7.点差法
只要是中点弦问题,就用点差法。

(三)与直线相交
必考题,且每年形式基本一致,先从理论上说说这道题的解题步骤。
步骤1:先考虑直线斜率不存在的情况。求结果。(此过程仅需很简短的过程)
步骤2:设直线解析式为 y=kx+b(随机应变,也可设为两点式)
步骤3:一般,所设直线具有某种特征,根据其特征,消去上式中k或b中的一个。
步骤4:联立直线方程和圆锥曲线方程,得到: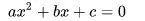
步骤5:求出判别式 △,令 △>0(先空着,必要时候再求 △>0 时的取值范围)
步骤6:利用韦达定理求出 x1x2,x1+x2(先空着,必要时再求y1y2)
步骤7:翻译题目,利用韦达定理的结果求出所求量。


函数与导数
导数这块的步骤也是固定的,导数与函数的题型,大体分为三类。
1.关于单调性,最值,极值的考察;
2.证明不等式;
3.函数中含有字母,分类讨论字母的取值范围;
无论是哪种题型,解题的流程只有一个,如下图所示。

例题比较简单,但是注意两点:一是任何导数题的核心步骤都是以上四部,二是时刻提醒自己定义域。以上例题属于第一类题型。
第二类题型,证明不等式,需要先移项,构造一个新函数,可以使不等号左边减去右边,构成的新函数,利用以上四个步骤分析新函数的最值与0的大小关系,可以得证。此为作差法。还有一种方法叫作商,即左边除以右边,其结果与1做对比。不过此方法不建议使用,因为分母有可能为0,或者正负号不确定。
还要注意逻辑。如果证明 A ≤ B,新函数设为 A - B,那么,需要 A- B的最大值小于等于0。
第三类问题,求字母的取值范围。先闭着眼睛当成已知数算,算完以后列表,针对列表中的结果进行分情况讨论。(一般,题目都会写明字母不为0)
以上就是为各位同学总结的题型和解题套路,并没有把所有的题型完整总结,只是提供一个思路和示范,此外下方还为大家整理归纳了高中数学100个核心考点,同学们可以按照这种模式自行总结。最后,重申三点:记住基础知识素材,总结题型,提取解题策略。
高中数学100个核心考点全汇总





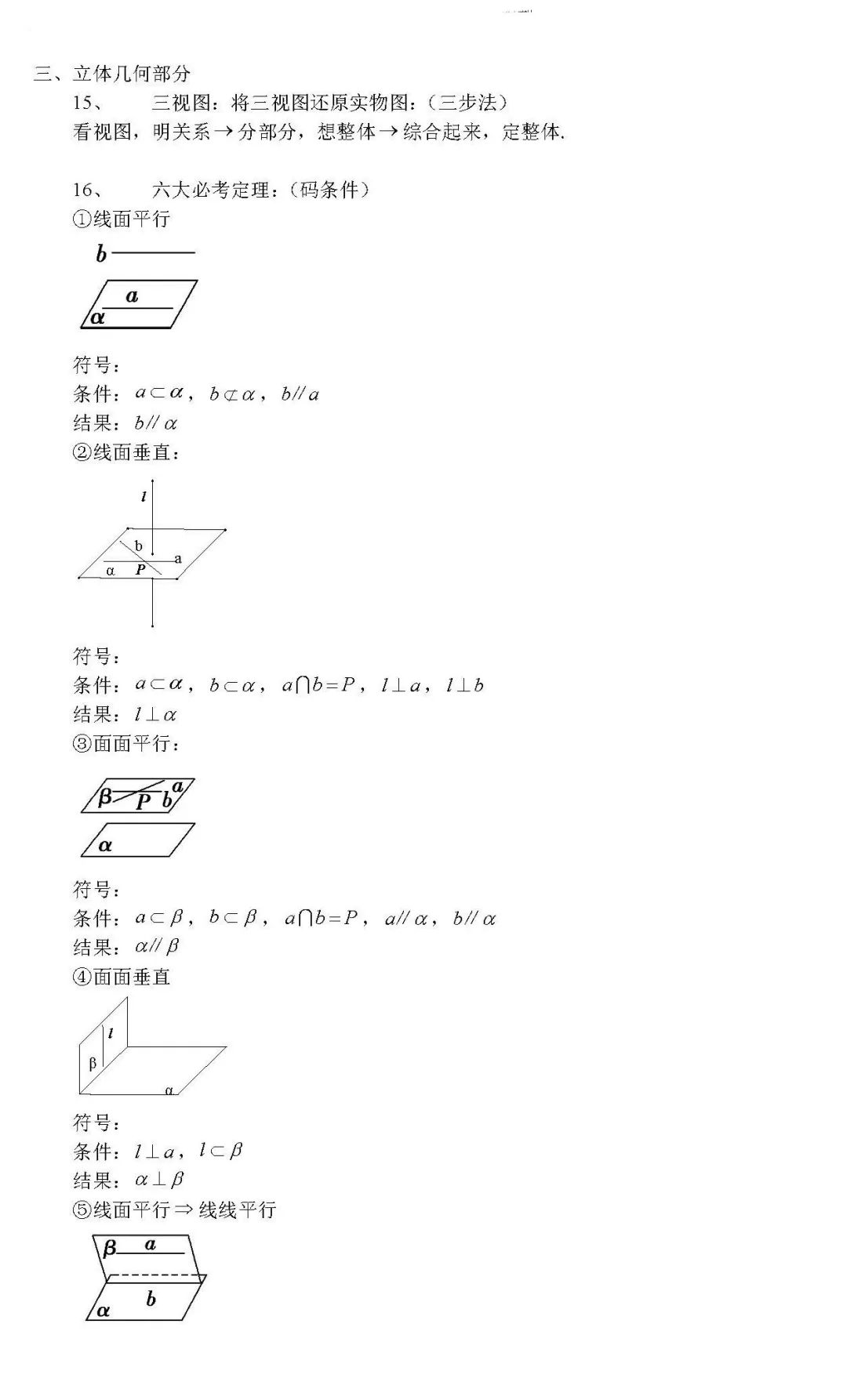









高中数学 高考数学 函数 高中数学 函数
















